认识博弈论

认识博弈论
ivansli何为博弈
在中国古文中,”博”的本意是六根筷子和十二枚棋子进行的赌输赢的一种游戏。谓之”六箸十二棋”,作为动词包含有”下棋”之意。”弈”指的是围棋。因此,从中文字面义来看,”博弈”就是指”下围棋”,再后来引申出"竞技"的概念。
在英文中,”博弈”对应的词是”game”,翻译为”游戏”,既有”消遣娱乐”,又有”按照规则进行的体力、智力竞赛”之意 (博弈论在英文中为:game theory)。
由此可知,中外基本一致的认识是:博弈是一种双方(多方)的对抗(竞技),对抗总是在一定的规则下进行,参与者必须考虑应对的策略,尽可能使自己获胜。
博弈论前世今生
博弈论的思想在国内外都有非常悠久的历史,无论是人们熟知的”田忌赛马”,还是《孙子兵法》、《圣经》、希腊神话等诸多传说,都蕴含着博弈的智慧思想。但是,博弈论不同于博弈,博弈论是对博弈的理论研究,通过对博弈的理论分析从而提升人们的博弈能力。
1944年,数学家约翰.冯诺依曼与经济学家奥斯卡.摩根斯坦合著的《博弈论与经济行为》标志着博弈论真正的作为一门学科理论的诞生,被称为”20世纪前半期最伟大的科学成就之一”。
真正把博弈论发扬光大的是数学家约翰.纳什(电影《美丽心灵》,讲述纳什的故事)在1950年和1951年连续发表的两篇关于非合作博弈论的论文,证明了非合作博弈均衡解的存在性,即著名的纳什均衡。
托马斯.谢林1960年出版的《冲突的战略》,一改之前博弈论公理化论述传统,从案例与故事出发,把博弈论介绍给社会大众,谢林开创了非数学博弈理论这一新的领域。他运用优美的语言和小模型,而非严格的逻辑论证,将他的理论通过众多的实际应用分析表述出来。
博弈论现如今在诸多领域中都有应用,例如:经济学、军事政治学、生物进化学、外交学、社会学等。
博弈论基本概念
博弈论的基本概念包含7个:
参与人
博弈中的决策主体,可以是一个自然人也可以是一个企业或者组织行动
参与人在博弈的某个时间节点的决策变量,行动空间限制了参与人的选择范围,告诉参与人什么事情可以做。信息
博弈中每个参与人都知道什么策略
规定了参与人在什么情况下应该如何行动,参与人在行动之前准备的一套完整的行动方案或预案支付(payoff)/得益/损益 [注意:中文有多种叫法,大多数书中用支付一词]
每个参与人在给定的策略组合下得到的报酬、收益均衡
博弈的一种稳定状态,在该状态下所有参与人都不再愿意单方面变更自己的策略结果
参与人和分析者所关心的博弈均衡情况下所出现的东西,
博弈论前提假设
博弈论有着特色鲜明的前提假设,主要包括三方个:
每一个参与人是工具理性的
理性人要有一个明确的偏好,在给定的条件下,能够追求自我偏好的最大化。
理性又分为:个体理性、集体理性(帕累托效率)“每一个参与人是工具理性的”这一点是所有参与人的共同知识
一般理性共识是无穷阶次的理性共识 (让我想起三体中的猜疑链也是无穷阶次)所有参与人都了解博弈的规则
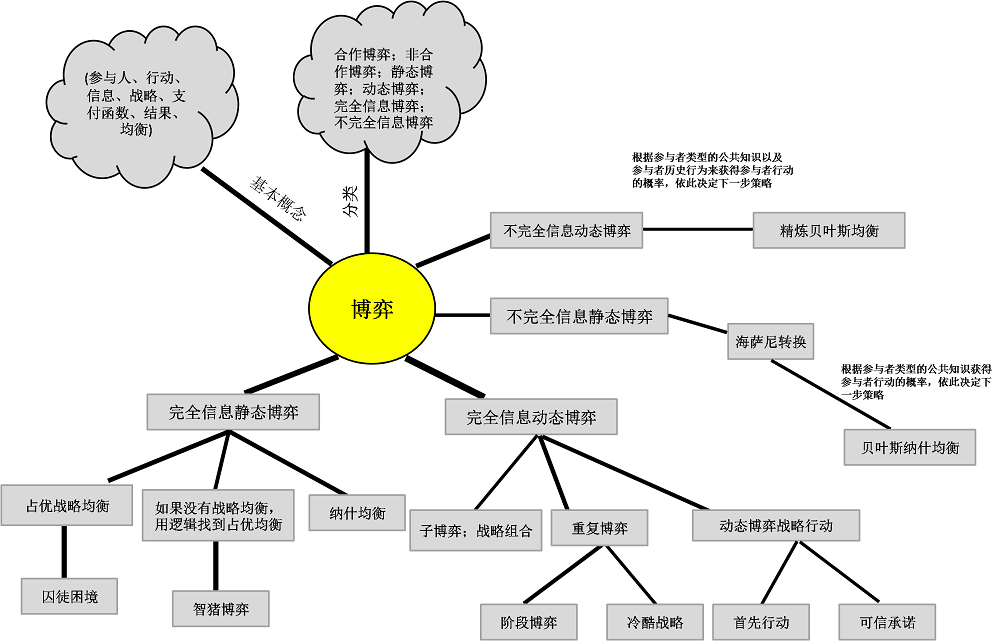
博弈论分类
按照参与人做出策略与行动的先后次序分为:
- 静态博弈
- 动态博弈
按照参与人对其他参与人的了解程度分为:
- 完全信息博弈
- 不完全信息博弈
按照参与人是否能够达成一种具有约束力的协议分为:
- 合作博弈
- 非合作博弈
按照博弈结果的损益分为:
- 零和博弈 (又称:常和博弈)
- 非零和博弈 (又分为:正和博弈、负和博弈)
按照博弈的次数分为:
- 一次博弈
- 重复博弈 (分为:有限次重复博弈、无限次重复博弈)
经典博弈分类以及对应均衡
| 行动顺序 | 信息 | |
| 完全信息 | 不完全信息 | |
| 静态博弈 | 完全信息静态博弈 (纳什均衡) |
不完全信息静态博弈 (贝叶斯纳什均衡) |
| 动态博弈 | 完全信息动态博弈 (子博弈精炼纳什均衡) |
不完全信息静态博弈 (精炼贝叶斯纳什均衡) |
纳什均衡
纳什均衡是所有参与人的最优策略组合,在这一组合中,没有任何人有积极性改变自己的选择。
纳什均衡在博弈中出现的次数基本为奇数个(有数学证明),即:1个、3个、5个…,博弈最终结果会是出现的纳什均衡中的某一个。
纳什均衡根据某一特定策略出现的概率分为:
- 纯策略纳什均衡
- 混合策略纳什均衡
纯策略纳什均衡是混合策略纳什均衡的退化,是混合策略纳什均衡的一种特例。
例如说,参与人A在博弈中有2种策略可供选择A1、A2:
① 如果A分别以一定的概率(概率之和为1)选择策略A1(50%选择)、A2(50%选择),则A的策略则为混合策略纳什均衡。
② 如果A选择策略A1(100%选择)、不选择A2(0%选择) 或者 不选择策略A1(0%选择)、选择A2(100%选择),则A的策略则为纯策略纳什均衡。
所以说,纯策略纳什均衡是混合策略纳什均衡的特例。
博弈论经典模型
在博弈论这门学科中有很多模型,其可以映射到社会的各个领域中的一些问题,并为解决问题提供理论支持。
博弈论经典模型:
囚徒困境
个体理性选择从而导致集体理性(利益)受损懦夫(胆小鬼)博弈
大国博弈的均衡解夫妻博弈
合作博弈智猪博弈
搭便车行为兔鹿博弈
通过沟通促进合作,从而创造更大的价值监督博弈
企业中老板要不要监督,员工要不要偷懒征税博弈
纳税人要不要偷税,税务机关要不要检查、加大惩罚蜈蚣博弈
合作双赢,不合作单赢万元陷阱
及时止损的重要性……
博弈论常用分析方法
一般来说,在博弈论的分析中使用得益(通常是数字)来标识某种特定策略给参与人造成的得失,作为理性人会根据不同的得益来选择不同的策略。
博弈论经常使用的两种表述(分析)的方法,分别是:
- 得益矩阵(博弈论的标准式)
- 博弈树(博弈论的扩展式)
以囚徒困境模型为例,分析使用得益矩阵与博弈树来描述其策略和得益情况。
囚徒困境:警察抓到甲、乙两个小偷,把他们两个分开关押,同时让他们交代自己与对方的过往犯罪记录。如果自己坦白而对方抗拒,则自己不坐牢,对方坐牢10年。如果都坦白,则分别坐牢8年。如果都抗拒,则分别坐牢1年。问:最终这两个小偷会如何选择自己的策略?
(用数字来表示损益,坐牢1年用-1表示,不坐牢用0表示。第一个数字代表甲的损益,第二个数字代表乙的损益)
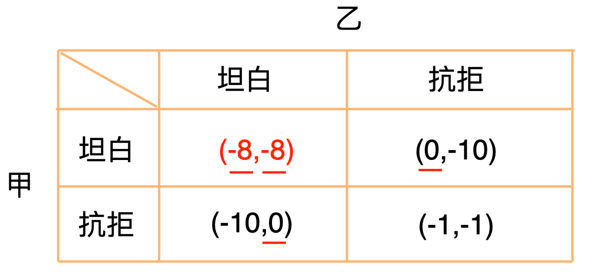
得益矩阵表示法
注:得益矩阵常用排除劣策略、划线法等手段来分析并寻找均衡点
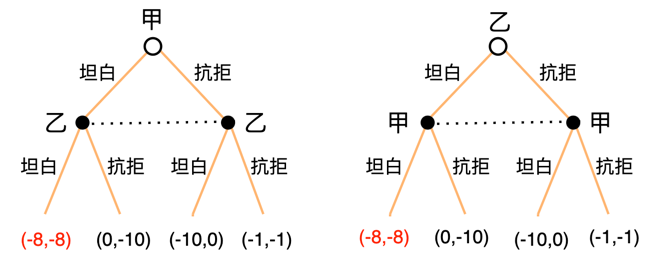
博弈树表示法
注:①博弈树中的虚线被称为信息线:表示参与人在这里不知道自己应该选择哪个节点,即:不知道对方的策略是什么 ②节点代表参与人此处需要做出抉择 ③空心节点表示初始节点 ④节点发出的线代表参与人的一种策略
如上所示的囚徒困境,通过博弈论分析最终得出:囚徒甲、乙分别处于个体的理性的考虑都选择坦白的策略(整个博弈只存在一个纳什均衡),即:(甲坦白,乙坦白),而没有选择最优的 (甲抗拒,乙抗拒),因此(甲坦白,乙坦白)策略组合也是纳什均衡点。囚徒困境是典型的个体理性导致集体非理性的模型(亦可用此模型分析职场中的”卷”,家长疯狂的给孩子报兴趣班等现象)。
简述博弈论的重要性
协调与合作是社会面临的两个问题,如何通过有效的分析从而选择合适的策略,并达到集体理性,并创造更大的社会整体价值,这是博弈论需要做的事情。对于博弈论这门学科来说,其价值远非如此简单。小到日常选择大到国家事务,都有它的身影。
推荐书籍
- 《博弈与社会》张维迎
- 《博弈论》蒋文华
- 《自私的基因》理查德·道金斯