博弈论对一般问题的建模分析

博弈论对一般问题的建模分析
ivansli博弈论是一门基于数学为基础的学科,在使用其分析现实问题的过程中,往往需要针对具体问题建立模型,并根据模型显示的不同策略对应的得益值进行抉择,进而取得均衡解。本文以绑架问题为例,简述建模分析过程。
常用建模分析步骤
常见建模分析过程大致分为4步,具体如下所示:
第1步:确定参与人
第2步:选定参与人所用策略
第3步:罗列结局,按偏好排序并赋予得益(损益/支付)值
第4步:比较得益,找出(计算)均衡解
绑架问题的建模分析
问题描述:你的家人被绑匪绑架,绑匪向你索要赎金,答应拿到赎金后才能放人。此时你应该如何决策?
绑架问题建模分析过程如下:
第1步:确定参与人
你(被绑架的家人此时由于并没有决策能力,所以不属于参与人)、绑匪
第2步:选定参与人所用策略
你:交赎金、不交赎金
绑匪:放人、撕票
第3步:罗列结局,按偏好排序并赋予得益(损益/支付)值
这个博弈共有4个结局:不交赎金放人、交赎金放人、不交赎金撕票、交赎金撕票
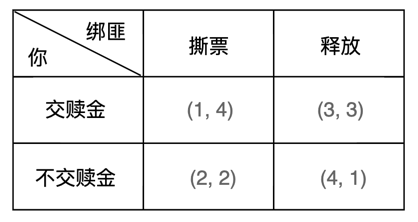
对于你来说,面对上述4个结局需要你根据预期偏好进行排序,作为一个理智的人一般会得到如下次序:不交赎金放人 > 交赎金放人 > 不交赎金撕票 > 交赎金撕票。排好序之后,针对每一种结果赋予得益值,得益值必须能反馈出你的偏好次序(即:具体的得益值并不太重要)。假设,最终你的得益值如下:
①不交赎金,绑匪放人 4分
②交赎金,绑匪放人 3分
③不交赎金,绑匪撕票 2分
④交赎金,绑匪撕票 1分
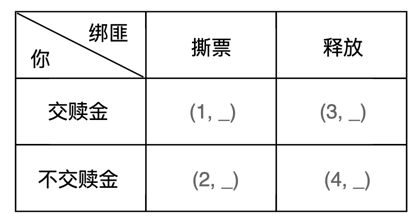
对于劫匪来说,面对上述4个结局也需要根据绑匪的预期偏好进行排序。劫匪会如何进行排序呢?那么,就需要你根据绑匪的偏好进行判断。此时,你面临2种情况,情况1你熟悉绑匪的风格以及偏好(即:完全信息博弈),情况2你不熟悉绑匪的风格以及偏好(即:不完全信息博弈)。现实生活中,大部分是不完全信息,再加上此时面对家人受到威胁,想必更多的是不完全信息博弈。即:面对着的是一个你并不熟悉其的风格以及偏好的绑匪。
此时,你需要做的就是把绑匪可能出现的类型都罗列出来进行分析。绑匪又分为3种类型:存有良知型、金钱至上型、残暴型。
存有良知型绑匪,以得到赎金为目的,如果得不到赎金也愿意放人(关心的是什么情况下放人)。其偏好次序:交赎金放人 > 不交赎金放人 > 交赎金撕票 > 不交赎金撕票。得益值如下:
①交赎金,绑匪放人 4分
②交付赎金,绑匪放人 3分
③交赎金,绑匪撕票 2分
④不交赎金,绑匪撕票 1分
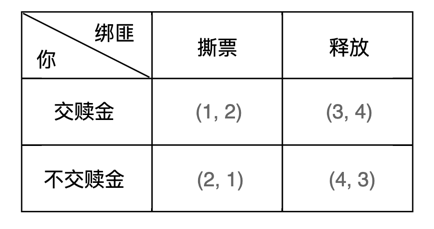
金钱至上型绑匪,目标是讹诈赎金,交赎金会放人,以免被抓到罪加一等。不交赎金会撕票,以确保以后其他绑架还可信(关心的是赎金)。其偏好次序:交赎金放人 > 交赎金撕票 > 不交赎金撕票 > 不交赎金放人。得益值如下:
①交赎金,绑匪放人 4分
②交赎金,绑匪撕票 3分
③不交赎金,绑匪撕票 2分
④不交赎金,绑匪放人 1分
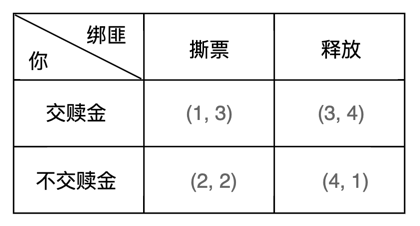
残暴型绑匪,无论是否付赎金都会选择撕票(关心的是赎金)。其偏好次序:交赎金撕票 > 交赎金放人 > 不交赎金撕票 > 不交赎金放人。得益值如下:
①交赎金,绑匪撕票 4分
②交赎金,绑匪放人 3分
③不交赎金,绑匪撕票 2分
④不交赎金,绑匪放人 1分
第4步:比较得益,找出(计算)均衡解
根据第3步可知,你面对的是3种类型绑匪的1种,使用得益矩阵,我们得出3种模型。
存有良知型绑匪,博弈的纳什均衡为:不交赎金,绑匪放人。
金钱至上型绑匪,博弈的纳什均衡为:不交赎金,绑匪撕票。
残暴型绑匪,博弈的纳什均衡为:不交赎金,绑匪撕票。
博弈结果分析
分析上述结论可知,除了残暴型绑匪之外,金钱至上型绑匪也出现了撕票。那么问题出在哪里?出在你的身上!
因为,你的偏好次序:不交赎金放人 > 交赎金放人 > 不交赎金撕票 > 交赎金撕票。其中,你认为不交赎金优于交赎金。一般而言这也无可厚非,任何一个人都希望既不花钱也能释放人质。问题是,如果每个人都这样想,也就不会出现富豪家人被绑架时花钱赎人的情况。
如果想要改变博弈结果,参与人必须改变自己的偏好。假设你此时认为交赎金优于不交赎金,则偏好次序为(无论是否撕票,交赎金排前面):交赎金放人 > 交赎金撕票 > 不交赎金放人 > 不交赎金撕票。
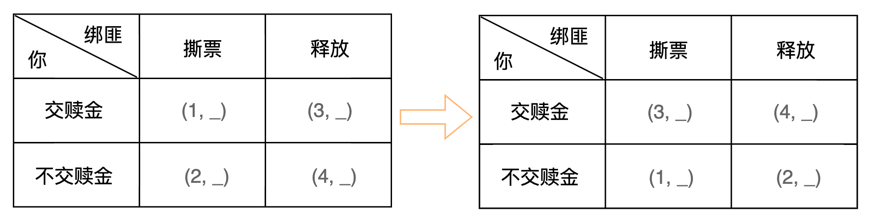
当你的偏好改为交赎金优于不交赎金后,将新的得益值代入上述3种绑匪的博弈矩阵之后,得到的博弈结果为:
存有良知型绑匪,博弈的纳什均衡为:不交赎金,绑匪放人。
金钱至上型绑匪,博弈的纳什均衡为:交赎金,绑匪放人。
残暴型绑匪,博弈的纳什均衡为:不交赎金,绑匪撕票。
总结
实际情况远比上述分析过程更复杂,这里仅描述了面对实际情况应该如何建模分析。其次需要说明的是,博弈论是使用数学手段研究博弈过程中出现的策略、得益(支付),进而得出均衡解。
注:本文案例内容引用自《博弈论》蒋文华