二人零和博弈与最大最小定理

ivansli2023-10-072024-07-08

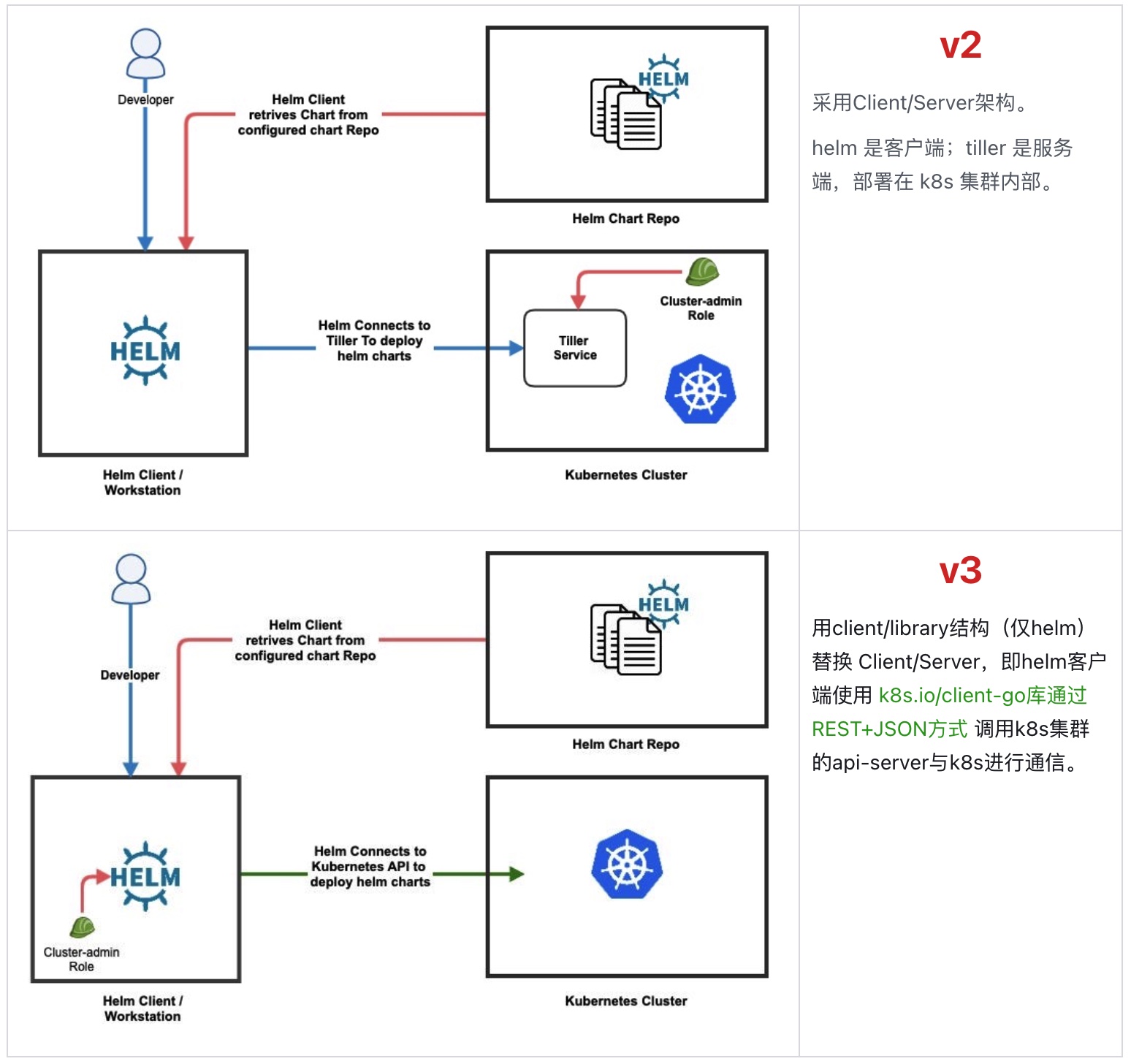
在博弈论的常见分类中，按照博弈前后的得益总和是否发生变化分为：零和(常和)博弈、非零和博弈。
零和博弈可以定义为：博弈前的得益总和与博弈后的得益总和相等(也有称为常和博弈)，博弈过程只是得益在不同的参与人之间重新分配。日常生活中，下棋、打牌、赌博都属于零和博弈，即一人所得为另一人所失。以打牌为例，桌子周围的钱是固定的金额，若要你赢得一些钱，其他人就必须输掉同等金额的钱。

二人零和博弈

在博弈论中，博弈中的参与人(可以是个人，也可以是能够做出统一决策的团体)至少是2人。为了简化博弈的分析过程，通常指定参与人为2人。二人零和博弈，就是指有2个参与人的博弈，其博弈前后的得益总和固定不变，即一方所得为另一方所失。
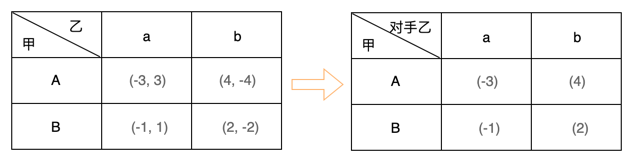
一般为了方便计算，会进一步简化博弈过程的得益值，2个参与人的得益之和相加等于0。由于二人零和博弈中一人所得为另一人所失，那么作为相互竞争的对手。一个参与人希望在所有的得益中取得最大值，那么其对手就会希望对方取得最小值(对方越少，自己所得就越多)。在使用最大最小定理的时候，可以再次把得益简化为只剩下一方的得益。

最大最小定理

最大最小定理是冯诺依曼在博弈论中提出的最重要和最基础的一个定理，该定理表明，为一个有限的二人零和博弈赋予一个值V：在双方理性行动的前提下，参与人1预期能够从参与人2那里赢取的平均盈利。冯诺依曼认为用这种方法预测结果是可行的，原因如下：
1.有某个策略，可以确保参与人1获得盈利V，参与人2的任何行动都无法阻止。因此，参与人1不会接受小于V的盈利。
2.有某个策略，可以确保参与人2的平均损失不会超过V，即可以防止参与人1获得超过V的盈利。
3.根据假设，博弈是零和的，参与人1的盈利是参与人2的损失，因为参与人2希望损失最小，他会把参与人1的平均盈利限制在V。(在非零和博弈中不成立)

在计算得益时，最大最小定理分为：最大化最小值，最小化最大值。

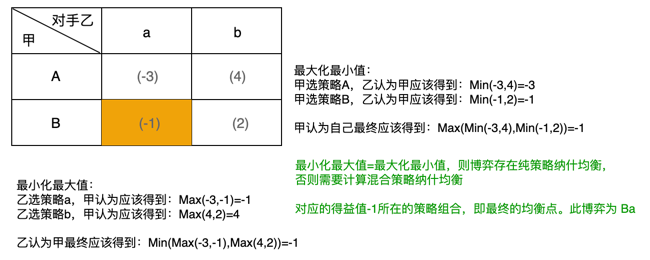
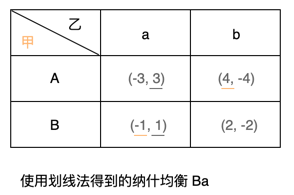
最大化最小值可以理解为：你的对手在某些策略下为了减少自己的损失只允许你挑选最小的得益，在策略空间内会得到一组最小的得益。但是你为了使自己能获得最大的盈利，会在这组得益中挑选最大的值作为自己的最终得益，即:你的最终得益=你Max(对手Min(...得益...))。在对得益矩阵进行计算时，取每一行的最小值，然后再对这些最小值取最大值。
最小化最大值可以理解为：你自己在某些策略下为了确保自己的盈利只挑选最大的得益，在策略空间内会得到一组最大的得益。但是你的对手为了减少自己的损失，会在这组得益中挑选最小的值作为你的最终得益，即:你的最终得益=对手Min(你Max(...得益...))。在对得益矩阵进行计算时，取每一列的最大值，然后再对这些最大值取最小值。

求解二人零和博弈的方法

求解一个二人零和博弈，应该使用以下几个步骤：
1.计算最大化最小值和最小化最大值，若这两值相等，就找到了合适的策略，并且能计算出博弈值。若不相等，进入第二步。
2.剔除所有劣策略。
3.为你的每一个策略都指定一个概率值，保证无论你的对手做什么，最终他得到的平均盈利都一样。假定你的对手也这样做。如果你采用混合策略得到的盈利等于对手采用的混合策略得到的盈利，且概率值不为负数时，就得到了博弈的解。如果这两个盈利不等，或出现负数概率，重新检查劣策略。如果不存在劣策略，那么这种方法就失效了。